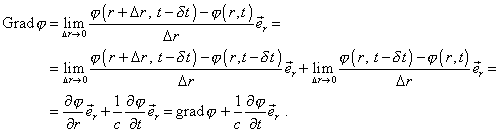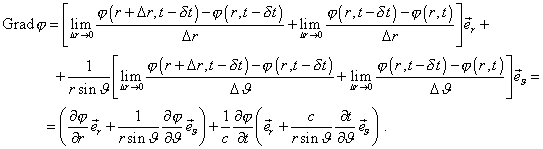Я очень уважаю указанных вами авторов, "но истина дороже".
И так из определения имеем:
1. Градиентом называется действие векторного оператора набла на скаляр.
gradφ ≡ ∇φ.
2. Действие векторного оператора набла на вектор, согласно правилам векторного анализа возможен только в двух видах.
А именно:
а. Скалярное произведение векторного оператора на вектор есть дивергенция вектора
divF ≡ (∇ ⋅ F);
б. Векторное произведение векторного оператора набла на вектор есть ротор вектора.
rotF ≡ [∇ × F].
А градиент вектора, это как?

Это определения из векторного анализа. Мы же имеем дело с тензорным.
Про градиент вектора мне лучше Википедии не сказать.

Т.е. Вы хотите сказать, что могут быть два правильных математических аппарата получающих два разных, но правильных решения?

Получается весьма своеобразная ситуация.
Векторное исчисление и векторный анализ операцию градиент вектора исключают, но тем не менее она фигурирует в математических манипуляциях не имея никакого геометрического смысла.
Слово за математиками...

Я думаю, а Paraligon меня поправит, что градиент вектора можно определить в виде якобиана так:
[dmath]\partial \vec A=\frac {\partial (A_1, A_2, A_3)}{\partial (x_1, x_2, x_3)}= \begin{pmatrix}
\partial_1 A_1 & \partial_1 A_2 & \partial_1 A_3 \\
\partial_2 A_1 & \partial_2 A_2 & \partial_2 A_3 \\
\partial_3 A_1 & \partial_3 A_2 & \partial_3 A_3
\end{pmatrix}[/dmath]
След его является дивергенцией вектора А, а недиагональные члены можно представить как ротор вектора А, в котором [imath](\nabla \times \vec A)_3 =\partial_1 A_2-\partial_2 A_1[/imath] + циклические перестановки индексов.


Это одно и тоже, но по-разному представленные.

Векторный анализ - это тоже тензорный анализ, только более общий. Для 3D пространства в нём есть специфика, связанная с векторным произведением, которая очень хорошо описана в книге Новикова и др.

Поэтому, в частности, в 4D нельзя ввести векторное произведение и ротор так просто, как в 3D.

Если я Вас правильно понял, Вы хотите сказать, что градиент вектора можно представить как ротор вектора или/и дивергенцию вектора?
Я Вас правильно понял?

Да, всё верно. Якобиан - это более общий объект, чем дивергенция и ротор, потому что в нем есть все производные и причем он легко обобщается на любые размерности. Напр. в размерности 4 уже нельзя из него выделить 4-вектор, который бы обладал теми же свойствами, что и ротор. Так получается из-за того, что два таких вектора нормальны не одному направлению, как в 3D, а плоскости.

Поэтому наш Мир такой уникальный.

Обсуждается не "якобиан", а получившая широкое распространение операция "градиент вектора".
По определению градиент есть вектор характеризующий величину возрастания функции в направлении наибольшего её возрастания.
Как может дивергенция (скаляр) быть вектором?

Эта операция широко применяется в тензорном анализе. В векторном её нет. Поэтому дивергенция, как и след якобиана, - скаляр.

Можно, наверное, говорить о градиенте вектора в векторном анализе тоже, но понимая, что это ротор и дивергенция в одном флаконе - потому что, как я уже сказал, векторный анализ - это раздел тензорного.

Если это ротор и дивергенция в одном флаконе, то эта операция некорректна и недопустима как в векторной, так и в тензорной форме в силу требования тождественности отображения в любых различных математических системах.

Ув. Зиновий. Во-первых, я сказал "наверное". Во-вторых, никто не запрещает использовать градиент применительно только к скалярам.

Просто в тензорном анализе используется более широкое определение. Можно ведь расписать градиенты для каждой компоненты вектора, считая их скалярами, и назвать получившуюся матрицу Якоби градиентом вектора. Точно также и можно получить определение для градиента тензора любого ранга.

При этом, ещё раз подчеркну, ротор и дивергенция получаются из градиента вектора лишь в 3D. Лишь в трёхмерном евклиде можно так ввести аксиальный вектор, что он будет нормально расположен к двум другим полярным векторам.

В общем, я надеюсь, Вы мне поставите трояк по математике. Всё, что я знал на эту тему, я выложил.

Что значит "не запрещает использовать градиент применительно только к скалярам"?
Математическая корректность запрещает использовать оператор "градиент" к векторам согласно определению.

В этом и заключается ошибка математиков спутавших геометрию с алгеброй функций многих переменных.

Дело в том, что операторы "grad", "div", "rot" являются геометрическими пространственными инвариантами, характеризуя положение физических объектов в нём и становятся абсолютно бессмысленными в произвольном алгебраическом пространстве.

Я не ставил перед собой цель экзаменовать Вас, но хотел обратить ваше внимание и внимание заинтересованных специалистов в ошибочности использования геометрических операторов "grad", "div", "rot" в решении алгебраических задач функций не пространственных переменных.
Задачи с числом пространственных переменных больше 3-ёх не являются геометрическими и потому применение в них геометрических операторов неправомочно.

Здравствуйте уважаемый Зиновий.
Зарегистрировался, когда у видел, что теперь вы тут модератор.

Для меня основным является определение !.
Для потенциального гравитационного поля функция поля U = GMm/R Размерность кг*метр²/сек² - джоуль, скаляр.
Градиент это производная (dGMm/R)/dr = -GMm/R² = -ma вектор к центру сферы.
Запись для потенциала U = GM/R не корректна.

А что такое градиент вектора.
Чтобы была производная, надо чтобы он был переменным.
Например на плоскости модуль R = C*T угол Fi = w*T Угловая скорость на время.
Производная по времени даст вектор С + вектор W
Вектора взаимно перпендикулярны.

Складывать такие вектора я не умею.
Если конец вектора масса m, то могу сложить энергию E = mC²/2 + JW²/2
Энергия поступательно-вращательного движения.

Перемножавшие даcт третий вектор. Перпендикулярный плоскости этих двух.
А в объемных координатах, будет четвертое иизмерение?

Энергии без массы не бывает.
Так что там в электродинамике Максвелла вращается?
Фиктивный вектор тока?

Друзья, вы все здесь правы и не правы одновременно, а всё потому, что математика - это искусство называть одни и теже вещи разными именами (с) ...

По существу темы, нечто вразумительное можно почитать по ссылке:

https://ru.m.wikipedia.org/wiki/Оператор_набла

Посетить мою домашнюю страницу


Хотя и там написана, в большей части, "абстрактная чепуха" (с) ... поразительно, но в теме о Числах мы всё это уже разбирали достаточно подробно ...

Вот скажем это



Действительно, в математике ОПРЕДЕЛЕНИЕ просто обязано быть предельно корректным и точным ... вот, например, по той же ссылке, которую я привёл выше, авторы рассуждают о каких-то операторах, забывая, что ОПЕРАТОР это синоним слова ОТОБРАЖЕНИЕ, и не более того, а что такое ОТОБРАЖЕНИЕ F в категории множеств это специального типа ОТНОШЕНИЕ, которое для наглядности принято записывать так:

F: X --> Y

И из этой записи нельзя ничего опустить ... нельзя сказать "просто оператор F", не указывая область определения оператора X и область его значений Y ... ибо,

F: A --> B

это будет ДРУГОЙ оператор, если только X или Y отличаются от A или В, соответственно, хотя бы даже одним элементом (точкой) ... тем более нелепо выглядит описание "оператора" "набла" без указания области определения и области его значений ... именно отсюда идут "оправдания" его использования как удобного символа некоторого "исчисления" ... такая метода восходит ещё к дифференциальному и интегральному ИСЧИСЛЕНИЮ Лейбница и Ньютона, когда выучив несколько табличных правил, можно "брать" производные и интегралы не зная что это такое, но так происходит до поры до времени, пока мы не сталкиваемся в тех же задачах естествознания с ситуацией что исчисление не работает для функций недифференцируемых (с "уголками") разрывных и т.п. всё это возникает уже в электротехнике (функция Хевисайда, дельта функция и т.п.), в том числе, и в так называемой теории поля, векторном анализе, а в новейшее время в Нелинейном Анализе и т.п. ...

Как вы тут ссылки вставляете? ... :(

Гиперссылки не работают ... чтобы посмотреть копируйте ссылку и вставляйте в строку браузера ... плохо ...

Не понял юмора - почему в одних темах (например, о Числах) ссылки вставляются простым копированием, а здесь не вставляется ...

Я здесь подправил. Вы наверное, поторопились со ссылками.

vps137, спасибо, Друг! Я думаю, что большинство математиков ничего не понимают в связном наборе слов "векторный дифференциальный оператор" ... если кто и понимает, то требуется гораздо больше слов, чем написано в вики ...

Вот именно, создавать птичий язык, догматизируя то, что достигнуто моделированием в физике и устраивая из этого пляски абстракции ан костях познания.
В динамике градиент/оператор набла имеет вид

О градиенте потенциальной функции
Это выражение получается физическим моделированием, но не может быть получено абстрактными математическими ухищрениями.
При этом в динамике уже стандартное применение математических операторов
rotgrad φ ≠ 0
И весь птичий язык переходит в пустое карканье.
Развитие же математики возможно не придумыванием заумных слов, чем она, собственно, так увлеклась, а решением до сих пор не решённых задач в физике. Только тогда будет здоровое развитие, а не самолюбование.

Здесь, Сергей, Вы, похоже, изобрели велосипед.

Есть в математике понятие полной производной, которое близко к тому, что в Вас написано.
[dmath] \frac {d \phi}{dt}=\dot \phi+(\vec u \cdot \nabla) \phi[/dmath]
Если положить скорость u постоянной и равной c, то приходим к Вашему выражению. ([imath]\dot \phi=\frac{\partial \phi}{\partial t}[/imath])

Вот видите, как Вы переворачиваете, забыв, что в градиенте потенциала используются уже частные производные...
∇ = ex ∂ ∂x + ey ∂ ∂y + ez ∂ ∂z
Что Вы можете после этого решить? Да, ничего. Только плескаться в догмате, играя словами.
А между тем, если источник поля движется, будет уже другая формула...

Это тогда уж берите выше - ковариантная производная.

Опять игры в слова... Далее начнёте пространства изгибать, символы поднимать/опускать символом Кроннекера и проч.
И здесь ковариантная?

Это для движущегося источника (с. 7 статьи)
А с учётом трансцендентного уравнения для самого запаздывания и этого не запишешь...
А Вы говорите - велосипед... Ручка отмахнутая, а не велосипед..

Тот же член, только вид сбоку. Я про член Вашего уравнения.
То же самое, только с сферических координатах.

Вообще - гнаться за математиками - пустое дело.


Сергей из Харькова в чём-то прав. Математики пишут для себя на своём языке. Нужен транслятор с вашего "птичьего языка" хотя бы на тот, который был бы понятен рядовому физику.

Прежде чем фантазировать, надо изучить математический аппарат классической теории поля.
Оператор набла есть оператор в частных производных по пространственным координатам, если Вам это что ни будь говорит...

Прежде чем критиковать, нужно понять что сделано. У меня Grad и есть по пространственным координатам, а если Вы даже приведенные выводы не понимаете, то какие ко мне претензии? Выучите математику и тогда вопросов не будет.



Я и не гонюсь за математиками, только не обратили Вы внимание, что в приведенной формуле производная от единичного вектора по углу... :-)



Если бы математики что-то ещё получали ценное для физики, кроме птичьего языка... А то, если перевести, то получается обычная высшая математика, аналитическая геометрия и не более того. Всё остальное отфонарь.

У Вас "Grad" взят из безграмотной ТО Эйнштейна, что противоречит фундаментальным положениям векторного анализа.
Согласно векторному анализу частная производная по координатам берётся при постоянном времени.
Т.е. Δ t = 0.
Она потому и ЧАСТНАЯ ПО ПРОСТРАНСТВЕННЫМ КООРДИНАТАМ.

Послушайте, Зиновий, во-первых, в ТО такой формулы нет и никогда не было, как и не выводится она в рамках ТО. Во-вторых, прежде чем наезжать, ознакомились бы с выводом. Всё в рамках классического формализма и никаких релятивистских фетюлек. Нужно сначала знать моделирование, а не просто в догматы старых книжек тыкать.

Математика и есть язык, для кого-то птичьй, а для кого-то более точный (с) ...
В теме о Числа это всё разбиралось ... повторяемся ...

Вот пример грамотного математического текста

Ну, и что нового по сравнению с Высшей математикой, кроме новых "закорючек"? Иначе определяете выпуклость/вогнутость функции? Или верхнюю/нижнюю границу? Что добавили эти символы в математику?
Если, например, появились гиперболические функции, то это новые возможности, новый, физически ассоциативный формализм формализм. Если появились функции Бесселя, то это тоже прорыв в решении задач и новый, также физически ассоциативный формализм. А что, повторяю, дали закорючки, которых даже в Mathtype нет?

SBK, читайте внимательно, там всё написано русским языком , однако ...

Вы об этих функциях?

https://ru.m.wikipedia.org/wiki/Гиперболические_функции

Так я всё понял, что там написано. У меня проблем с математикой нет. Вы ответьте мне: что нового ввели данные символы по сравнению с известной высшей математикой? Какие реальные задачи решены?

Опять у Вас с тэгами математическая путаница - адрес надо вставлять в первое поле.

SBK, дружище, а вы определитесь, что в "высшей" математике раньше появляется из символов e^x=exp(x) или sup, тогда всё и встанет на свои места!
В теме числа уже рассказывалось об этом ...

А тут нечего определяться, уважаемый Paraligon. символ sup действительно из высшей математики (и без кавычек), но в приведенном Вами тексте целая совокупность других символов с понтом дела изрекающим что-то новое. Вот я и спрашиваю, что действительно нового дало введение этих симолов?

Даже не буду с вами спорить.
Как говорят в таких случаях "Вам можно на красный"...

Можно относиться так, как сочтёте, но спорить в отношении динамического градиента можно только в том случае, если Вы укажете несоответствие моделирования классическому формализму. А так... обвинять меня в релятивизме только из-за того, что в формуле появилась производная оп времени - дело несерьёзное. В законах индукции Максвелла тоже присутствует производная по времени и из этого тоже можно делать заключение, что Максвелл был релятивист . Тем более, что эти формулы он записал с потолка, на основе наводящих рассуждений.
Но дело всё в том, что если рассматривать динамику полей, то этот член появляется автоматически, как и релятивистский множитель присутствует в законе Доплера. Однако, тут релятивизмом и не пахнет.
Просто на рубеже 19-20 вв классическая физика вошла в область динамики, но остановилась на полпути, что отражено и в уравнениях Максвелла. Вот эта остановка и позволила вклиниться ревизионистам, создавшим некий каламбур из абстрактных предположений и тех неполных наработок, которые успела сделать классическая физика того времени. Отсюда и внешняя, отдалённая похожесть.
Мы просто пошли дальше и закончили процесс перехода в рамках классического формализма, получив наши решения, в которых нужно внимательно разбираться, а не отвергать из-за внешней похожести или отсутствия этих решений у классиков. Могу заверить, что все результаты получены нами строго в классическом формализме и это легко проверить, если, конечно, не отвергать с порога.
И закон Кулона, заложенный нами в постановку задачи для динамических полей тоже закономерен. Да, он статический, но обратите внимание на приведенную мной ранее запись динамического градиента. Там сумма статического градиента и динамического слагаемого. В наших диаграммах динамическое слагаемое учтёно комплексным запаздыванием. Так, как оно и возникает в теореме о динамическом градиенте. В результате получается совсем иная закономерность и в этом особенность динамики. Просто тут нужно вкопаться и всё становится на свои места.

Очень жаль, что Вы не будучи знакомым с историей вопроса, делаете умозрительные выводы исключительно исходя из уравнений Максвелла.
Задачу пространственного распределения и распространения возмущений в эфире решали и решили гораздо большие умы чем Максвелл.
Авторами были Гамельтон, Лаплас, Гельмгольц.
Максвелл только использовал готовый математический аппарат и притом неправильно.
Именно отсюда и ваши умозрительные и потому ошибочные выводы.
Откройте Корн-ов и изучите классическую теорию поля.

Лаплас занимался стационарными полями, Гельмгольц - частным случаем волнового уравнения, Гамильтон - энергетическим представлением в механике. Ни у кого не было решения наших задач. Корнов я Вам уже открывал. Хотите перебирать старые кубики? Ваши проблемы. Конечно, правильнее было бы Вам не предвзято вкопаться в вопрос, прежде чем авторитетами размахивать. НО это Ваше личное право, не так ли?

Математические фантазии ограничивает Математическая физика.
Что за физика в этом уравнении Максвелла?
Посмотрите в Вики...
[imath]\nabla \cdot \vec E = \frac {\partial {\vec B}}{\partial t}[/imath]

Пишут, что это "Закон магнитной индукции Фарадея", поясгяют "Изменение магнитной индукции порождает вихревое электрическое поле".[~ 1]

Но, в физике магнитная индукция дает вектор ЭДС, а не вектор напряженности электрического поля.
ЭДС движет электроны по проводнику, которые накапливаясь на концах проводника создают электрическое поле.

[imath]\nabla [/imath] дает вектора сил, действующих только в правой части прямоугольных координат.
У Максвелла такого ограничения, для его, якобы ЭМВ нет.
Да и у Фарадея нет. Хотя у него и наблы нет.

Эдс является следствием возбуждения тока в индуцируемом проводнике, а не причиной тока. Причиной он является во внешней цепи.
У Фарадея, как известно, вообще формул не было. Никаких. Чистый экспериментатор.

Оператор набла - оператор Гамильтона.
Даламбертиан - развитие Лапласиана на динамику.
Теория поля Гельмгольца - полное описание распределения и распространения физических как статических так и динамических полей в свободном пространстве.
Всё, что пишите Вы есть ваши личные фантазии основанные на незнании классической теории поля.
При этом Вы мните себе, что якобы Вы развили якобы не доделанную предшественниками теорию поля.
Вот откуда у Вас появилась частная производная по пространственным координатам содержащая частную производную по времени.

Это ваше личное мнение, или научное, что другие умели писать формулы, а Фарадей был неуч?
Ну насчет, что первично ЭДС, или ток, спорить не буду.
Как скажите, так и будет

Об этом говорил и Карцев. И я не говорил, что он был неуч, хотя, действительно не учился в школе. Он был превосходный экспериментатор. Гениальный экспериментатор. И популяризатор. Его лекции - образец и на уровне с Р.В. Полем.

Ну, как посчитаете... Я из тех, кто может строго доказывать.

По сравнению с "высшей" математикой, там написано, что неравенство Ки Фаня эквивалентно теореме Брауэра о неподвижной точке. Традиционно, теорема Брауэра не входит (не входила) в курс "высшей" математики, хотя её отдельные эквивалентные варианты и могут быть получены методами той самой "высшей" математики, например, из интегральной формулы Гаусса-Остроградского (формулы Сокса) ... а новые результаты, да почти вся математика XX века может быть отсюда выведена ... конкретно, вот например, существование равновесия по Нэшу для двух и более лиц в теории игр - здесь напрямую нагляднее использовать неравенство Ки Фаня, не прибегая к топологической терминологии ... этот результат настолько поразил экономистов, что последние даже вручили Нэшу нобелевскую премию за это его элементарное наблюдение молодости, хотя Джон фон Нейман и выразил ему некоторый скепсис, ибо первый решил этим методом задачу для двух игроков ... на следующей странице книги Обэна и Экланда вы найдёте и массу других примеров ... замечательный пример из естествознания, который получается этим методом это решение астрофизиком Чандрасекаром задачи об устойчивости белых карликов и тоже нобелевка ... хотя рогатый Нобель и не любил математиков ...
Да, и ваш скрытый спор об операторе набла, тоже легко разрешается с помощью ... формулы Стокса, которая тоже эквивалентна теореме Брауэра, а значит и неравенству Ки Фаня ... и я не шучу!

Говорите, доказал?

Равновесие Нэша
Вот и посмотрим, насколько это соответствует реальности в экономике
Взяли случай Генри Форда. Он принципиально изменил стратегию, сделав ставку на высокие зарплаты и механизацию. Никто из "игроков" до него не платил столько и так не организовывал труд рабочих. Что ему только ни делали: и по судам таскали, и в антисемиты записывали, и фабрики жгли. Сейчас массовое производство, пооперационный расчёт труда являются базой мирового производства. Никто не хотел, но все пошли именно в русле начинаний Форда, а он смог преодолеть сопротивление.
Взяли пример из игр. В играх заранее заложена определённая стратегия. Если ты её придерживаешься, как минимум, не проигрываешь, а выигрываешь тогда, когда знаешь наперёд эту стратегию и в определённые моменты отходишь от неё, когда программа или другой игрок пытаются тебя подставить на стандарте, имеющем второе решение, которое программа/игрок не учитывают вследствие своей ограниченности/заданности. Этим ты нарушаешь баланс и только от тебя зависит насколько правильно ты просчитал встречную сторону. "Кто не рискует, тот не пьёт шампанского"...
"Прошиб меня холодный пот
До косточки,
И я прошелся чуть вперед
По досточке.
Гляжу - размыли край ручьи
Весенние,
Там выезд есть из колеи -
Спасение!

Я грязью из-под шин плюю
В чужую эту колею.

Эй, вы, задние! Делай, как я.
Это значит - не надо за мной.
Колея эта - только моя!
Выбирайтесь своей колеей.
(В. Высоцкий Чужая колея)

Так что, как известно, Нобеля дают не за успехи и знания, а за принадлежность к определённому клану. Нарушение баланса вопреки желанию других игроков - это основа победы в игре. И если победы реальность, то равновесие Нэша туфта.
А о Чандрасекаре вообще говорить нечего. Если он своим умом не допёр до элементарных ошибок в ОТО, его из школы выпускать не стоило, не то что нобелевские давать. Обычная безмозглая тасовка заданными корявыми кубиками. И то, что Нобелевский комитет этого не увидел, ещё раз говорит о его "уровне". К природе это не относится. Обычные игры чистого разума...

Математика, а тем более экономика, даёт нам множество различных состояний равновесия (Парето, Вальрас, Нэш и т.п.), но все они есть неподвижные точки, даже если они седловые как у Нэша.

Тайна присвоения нобелевок остаётся закрытой в течение 50 лет после их присвоения. Нэш получил свою за удачную модель для конечного числа игроков, даже не подозревая, что подобное равновесие может быть и в игре с бесконечным числом игроков ... в то время как в 50-е годы прошлого века для этого случая были получены только отрицательные результаты см. например В.Кли ...

Чандрасекар, конечно, получил свой результат о белых карликах исходя чисто из физических соображений ... лишь позднее было указано, что можно постооить модель, в которой равновесие белого карлика будет неподвижной точкой подходящего интегрального оператора ...

Настоящий оператор "набла" есть многозначный дифференциальный оператор (например, конус Кларка, субдифференциал и т.п.) ... на практике мы всегда имеем не одну касательную, а целый конус (пучок) касательных в тех точках, где нет привычной нам гладкости ... для выпуклого случая поведение такого дифференциала описывается в виде неравенстаа Ки Фаня ... которое по сути своей заменяет традиционное необходимое условие равенства нулю производной f'(x)=0

Я же Вам привёл абсурдность доказанного на двух примерах. Стоит ли гулять по всей физике, чтобы показать эти игры чистого разума в каждом случае.
Вот о белых карликах, предел массы которых якобы установил Чандрасекар.
"массы белых карликов составляют порядка солнечной, но размеры составляют лишь сотую (и даже меньше) часть солнечного радиуса, то есть плотность вещества в белых карликах чрезвычайно высока и составляет ρ~ 10⁵ - 10⁹ г/см³. При таких плотностях электронные оболочки атомов разрушаются, и вещество представляет собой электронно-ядерную плазму, причём её электронная составляющая представляет собой вырожденный электронный газ"
Физика и свойства белых карликов
Простой вопрос по школьной физике: если масса белых карликов сравнима с массой Солнца, почему само Солнца не белый карлик?
Второй не менее простой вопрос: как известно, давление к центру гравитирующего тела возрастает на несколько порядков? О какой средней плотности может идти речь? Тем более, о какой электронно-ядерной плазме, если у ангретого тела электроны уходят в оболочку, заряжая тело положительно, и это давно проверенный факт. Ещё и вырожденная электронная плазма там... Суют что зря в своих фантазиях...
Так что на этой базе считал Чандрасекар? То же, что и в своём двухтомнике по ЧД. А Вы всё за чистую монету принимаете. Тут физикой и не пахнет. Нет сил, которые могли бы сжать Солнце до белого карлика и Солнце тому прямое доказательство, а значит и любые пределы, посчитанные на этой основе тривиальная туфтица.
И пусть Нобелевский комитет скрывает свои тайны. По результату виден его уровень и без тайн.

Назначение темы чётко обозначено в названии темы.
Всё лишнее буду удалять.

Зиновий, градиент вектора это субдифференциал Кларка ...

Мне от этого не холодно и не жарко.
Покажите как должен в этом случае действовать оператор набла на вектор, при условии, что результат вектор?

Зиновий, ссылка в посте #2 темы, приведённая vps137 вполне удовлетворительная ... там прямо написана формула градиента для трёхмерного векторного поля (не скалярного!) ...

Упоминая субдифференциал Кларка, я лишь хотел сказать, что это понятие градиента можно написать даже для недифференцируемых полей ... конечно он становится многозначным отображением, но тем не менее сохраняет свои основные свойства в той форме, как они формулируются для таких отображений. В содержательной форме нашего дискурса следует остановиться на варианте приведённом vps137 ... это для того, чтобы я не вздумал объявлять градиент кограничным оператором, действующим на нульмерные дифференциальные формы (скаляры) и переводящим их в одномерные дифференциальные формы некоторого коцепного комплекса ...

Так что скажите, чем вас не устроила формула vps137 (или я уже это пропустил?)?

В связи с ответом vps137 я задал вопрос математикам.
Хотелось бы получить Ваш ответ.
Уточняю, речь идёт о реальных физических полях в физическом пространстве.