Градиент вектора, что это?, (математическая корректность операции!?) |

|
Здравствуйте, гость ( Вход | Регистрация )
Данный раздел форума предназначен для всевозможных дискуссий и обсуждений тем, касающихся науки и околонаучных вопросов. Ваши мысли, идеи, гипотезы и просто мнения - приветствуются, при условии соблюдения Правил раздела. И не забывайте регистрироваться.
  |
Градиент вектора, что это?, (математическая корректность операции!?) |
 9.2.2018, 20:49 9.2.2018, 20:49
Сообщение
#1
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7113 Регистрация: 7.10.2017 Из: г. Москва Пользователь №: 53225 |
Это определение градиента тензора приведено в книге Дубровина, Новикова, Фоменко Современная геометрия в самом начале гл. IV. Здесь его приводить из-за громоздкости нет смысла, потому что к нему надо было бы писать две страницы текста пояснений. Достаточно напомнить, наверное, что и скаляр, и вектор являются тоже тензорами. Я очень уважаю указанных вами авторов, "но истина дороже".И так из определения имеем: 1. Градиентом называется действие векторного оператора набла на скаляр. gradφ ≡ ∇φ. 2. Действие векторного оператора набла на вектор, согласно правилам векторного анализа возможен только в двух видах. А именно: а. Скалярное произведение векторного оператора на вектор есть дивергенция вектора divF ≡ (∇ ⋅ F); б. Векторное произведение векторного оператора набла на вектор есть ротор вектора. rotF ≡ [∇ × F]. А градиент вектора, это как? Сообщение отредактировал Зиновий - 5.3.2018, 21:28 -------------------- Тот кто не знает и/или не понимает определений физических понятий - не знает физики.
То кто не знает физики - не знает и не понимает жизнь. Природу изучать не формулы тачать. |

|
|
 10.2.2018, 5:03 10.2.2018, 5:03
Сообщение
#2
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7257 Регистрация: 12.8.2017 Пользователь №: 97485 |
Я очень уважаю указанных вами авторов, "но истина дороже". И так из определения имеем: 1. Градиентом называется действие векторного оператора набла на скаляр. gradφ ≡ ∇φ. 2. Действие векторного оператора набла на вектор, согласно правилам векторного анализа возможен только в двух видах. А именно: а. Скалярное произведение векторного оператора на вектор есть дивергенция вектора divF ≡ (∇ ⋅ F); б. Векторное произведение векторного оператора набла на вектор есть ротор вектора. rotF ≡ [∇ × F]. А градиент вектора, это как? Это определения из векторного анализа. Мы же имеем дело с тензорным. Про градиент вектора мне лучше Википедии не сказать. -------------------- Felix qui potuit rerum cognoscere causas. /Вергилий/
Апейроника - наука будущего? |

|
|
 10.2.2018, 10:51 10.2.2018, 10:51
Сообщение
#3
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7113 Регистрация: 7.10.2017 Из: г. Москва Пользователь №: 53225 |
Это определения из векторного анализа. Мы же имеем дело с тензорным. Т.е. Вы хотите сказать, что могут быть два правильных математических аппарата получающих два разных, но правильных решения?Про градиент вектора мне лучше Википедии не сказать. Получается весьма своеобразная ситуация.Векторное исчисление и векторный анализ операцию градиент вектора исключают, но тем не менее она фигурирует в математических манипуляциях не имея никакого геометрического смысла. Слово за математиками... Сообщение отредактировал Зиновий - 10.2.2018, 11:22 -------------------- Тот кто не знает и/или не понимает определений физических понятий - не знает физики.
То кто не знает физики - не знает и не понимает жизнь. Природу изучать не формулы тачать. |

|
|
 10.2.2018, 11:13 10.2.2018, 11:13
Сообщение
#4
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7257 Регистрация: 12.8.2017 Пользователь №: 97485 |
Я думаю, а Paraligon меня поправит, что градиент вектора можно определить в виде якобиана так:
[dmath]\partial \vec A=\frac {\partial (A_1, A_2, A_3)}{\partial (x_1, x_2, x_3)}= \begin{pmatrix} \partial_1 A_1 & \partial_1 A_2 & \partial_1 A_3 \\ \partial_2 A_1 & \partial_2 A_2 & \partial_2 A_3 \\ \partial_3 A_1 & \partial_3 A_2 & \partial_3 A_3 \end{pmatrix}[/dmath] След его является дивергенцией вектора А, а недиагональные члены можно представить как ротор вектора А, в котором [imath](\nabla \times \vec A)_3 =\partial_1 A_2-\partial_2 A_1[/imath] + циклические перестановки индексов. Т.е. Вы хотите сказать, что есть два правильных математических аппарата получающих два разных, но правильных решения? Это одно и тоже, но по-разному представленные. Цитата Получается весьма своеобразная ситуация. Векторное исчисление и векторный анализ операцию градиент вектора исключают, но тем не менее она фигурирует в математических манипуляциях не имея никакого геометрического смысла. Слово за математиками... Векторный анализ - это тоже тензорный анализ, только более общий. Для 3D пространства в нём есть специфика, связанная с векторным произведением, которая очень хорошо описана в книге Новикова и др. Поэтому, в частности, в 4D нельзя ввести векторное произведение и ротор так просто, как в 3D. Сообщение отредактировал vps137 - 10.2.2018, 11:22 -------------------- Felix qui potuit rerum cognoscere causas. /Вергилий/
Апейроника - наука будущего? |

|
|
 10.2.2018, 11:29 10.2.2018, 11:29
Сообщение
#5
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7113 Регистрация: 7.10.2017 Из: г. Москва Пользователь №: 53225 |
Я думаю, а Paraligon меня поправит, что градиент вектора можно определить в виде якобиана так: Если я Вас правильно понял, Вы хотите сказать, что градиент вектора можно представить как ротор вектора или/и дивергенцию вектора?[dmath]\partial \vec A=\frac {\partial (A_1, A_2, A_3)}{\partial (x_1, x_2, x_3)}= \begin{pmatrix} \partial_1 A_1 & \partial_1 A_2 & \partial_1 A_3 \\ \partial_2 A_1 & \partial_2 A_2 & \partial_2 A_3 \\ \partial_3 A_1 & \partial_3 A_2 & \partial_3 A_3 \end{pmatrix}[/dmath] След его является дивергенцией вектора А, а недиагональные члены можно представить как ротор вектора А, в котором [imath](\nabla \times \vec A)_3 =\partial_1 A_2-\partial_2 A_1[/imath] + циклические перестановки индексов. Это одно и тоже, но по-разному представленные. Векторный анализ - это тоже тензорный анализ, только более общий. Для 3D пространства в нём есть специфика, связанная с векторным произведением, которая очень хорошо описана в книге Новикова и др. Поэтому, в частности, в 4D нельзя ввести векторное произведение и ротор так просто, как в 3D. Я Вас правильно понял? -------------------- Тот кто не знает и/или не понимает определений физических понятий - не знает физики.
То кто не знает физики - не знает и не понимает жизнь. Природу изучать не формулы тачать. |

|
|
 10.2.2018, 12:54 10.2.2018, 12:54
Сообщение
#6
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7257 Регистрация: 12.8.2017 Пользователь №: 97485 |
Если я Вас правильно понял, Вы хотите сказать, что градиент вектора можно представить как ротор вектора или/и дивергенцию вектора? Я Вас правильно понял? Да, всё верно. Якобиан - это более общий объект, чем дивергенция и ротор, потому что в нем есть все производные и причем он легко обобщается на любые размерности. Напр. в размерности 4 уже нельзя из него выделить 4-вектор, который бы обладал теми же свойствами, что и ротор. Так получается из-за того, что два таких вектора нормальны не одному направлению, как в 3D, а плоскости. Поэтому наш Мир такой уникальный. -------------------- Felix qui potuit rerum cognoscere causas. /Вергилий/
Апейроника - наука будущего? |

|
|
 10.2.2018, 13:02 10.2.2018, 13:02
Сообщение
#7
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7113 Регистрация: 7.10.2017 Из: г. Москва Пользователь №: 53225 |
Да, всё верно. Якобиан - это более общий объект, чем дивергенция и ротор, потому что в нем есть все производные и причем он легко обобщается на любые размерности Обсуждается не "якобиан", а получившая широкое распространение операция "градиент вектора"............................................................... По определению градиент есть вектор характеризующий величину возрастания функции в направлении наибольшего её возрастания. Как может дивергенция (скаляр) быть вектором? Сообщение отредактировал Зиновий - 10.2.2018, 14:07 -------------------- Тот кто не знает и/или не понимает определений физических понятий - не знает физики.
То кто не знает физики - не знает и не понимает жизнь. Природу изучать не формулы тачать. |

|
|
 10.2.2018, 15:36 10.2.2018, 15:36
Сообщение
#8
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7257 Регистрация: 12.8.2017 Пользователь №: 97485 |
Обсуждается не "якобиан", а получившая широкое распространение операция "градиент вектора". По определению градиент есть вектор характеризующий величину возрастания функции в направлении наибольшего её возрастания. Как может дивергенция (скаляр) быть вектором? Эта операция широко применяется в тензорном анализе. В векторном её нет. Поэтому дивергенция, как и след якобиана, - скаляр. Можно, наверное, говорить о градиенте вектора в векторном анализе тоже, но понимая, что это ротор и дивергенция в одном флаконе - потому что, как я уже сказал, векторный анализ - это раздел тензорного. -------------------- Felix qui potuit rerum cognoscere causas. /Вергилий/
Апейроника - наука будущего? |

|
|
 10.2.2018, 15:52 10.2.2018, 15:52
Сообщение
#9
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7113 Регистрация: 7.10.2017 Из: г. Москва Пользователь №: 53225 |
Эта операция широко применяется в тензорном анализе. В векторном её нет. Поэтому дивергенция, как и след якобиана, - скаляр. Если это ротор и дивергенция в одном флаконе, то эта операция некорректна и недопустима как в векторной, так и в тензорной форме в силу требования тождественности отображения в любых различных математических системах.
Можно, наверное, говорить о градиенте вектора в векторном анализе тоже, но понимая, что это ротор и дивергенция в одном флаконе - потому что, как я уже сказал, векторный анализ - это раздел тензорного. Сообщение отредактировал Зиновий - 10.2.2018, 15:54 -------------------- Тот кто не знает и/или не понимает определений физических понятий - не знает физики.
То кто не знает физики - не знает и не понимает жизнь. Природу изучать не формулы тачать. |

|
|
 10.2.2018, 18:01 10.2.2018, 18:01
Сообщение
#10
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7257 Регистрация: 12.8.2017 Пользователь №: 97485 |
Если это ротор и дивергенция в одном флаконе, то эта операция некорректна и недопустима как в векторной, так и в тензорной форме в силу требования тождественности отображения в любых различных математических системах. Ув. Зиновий. Во-первых, я сказал "наверное". Во-вторых, никто не запрещает использовать градиент применительно только к скалярам. Просто в тензорном анализе используется более широкое определение. Можно ведь расписать градиенты для каждой компоненты вектора, считая их скалярами, и назвать получившуюся матрицу Якоби градиентом вектора. Точно также и можно получить определение для градиента тензора любого ранга. При этом, ещё раз подчеркну, ротор и дивергенция получаются из градиента вектора лишь в 3D. Лишь в трёхмерном евклиде можно так ввести аксиальный вектор, что он будет нормально расположен к двум другим полярным векторам. В общем, я надеюсь, Вы мне поставите трояк по математике. Всё, что я знал на эту тему, я выложил. -------------------- Felix qui potuit rerum cognoscere causas. /Вергилий/
Апейроника - наука будущего? |

|
|
 10.2.2018, 19:15 10.2.2018, 19:15
Сообщение
#11
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7113 Регистрация: 7.10.2017 Из: г. Москва Пользователь №: 53225 |
Ув. Зиновий. Во-первых, я сказал "наверное". Во-вторых, никто не запрещает использовать градиент применительно только к скалярам. Что значит "не запрещает использовать градиент применительно только к скалярам"?Математическая корректность запрещает использовать оператор "градиент" к векторам согласно определению. Просто в тензорном анализе используется более широкое определение. Можно ведь расписать градиенты для каждой компоненты вектора, считая их скалярами, и назвать получившуюся матрицу Якоби градиентом вектора. Точно также и можно получить определение для градиента тензора любого ранга. В этом и заключается ошибка математиков спутавших геометрию с алгеброй функций многих переменных.При этом, ещё раз подчеркну, ротор и дивергенция получаются из градиента вектора лишь в 3D. Лишь в трёхмерном евклиде можно так ввести аксиальный вектор, что он будет нормально расположен к двум другим полярным векторам. Дело в том, что операторы "grad", "div", "rot" являются геометрическими пространственными инвариантами, характеризуя положение физических объектов в нём и становятся абсолютно бессмысленными в произвольном алгебраическом пространстве. В общем, я надеюсь, Вы мне поставите трояк по математике. Всё, что я знал на эту тему, я выложил. Я не ставил перед собой цель экзаменовать Вас, но хотел обратить ваше внимание и внимание заинтересованных специалистов в ошибочности использования геометрических операторов "grad", "div", "rot" в решении алгебраических задач функций не пространственных переменных.Задачи с числом пространственных переменных больше 3-ёх не являются геометрическими и потому применение в них геометрических операторов неправомочно. Сообщение отредактировал Зиновий - 10.2.2018, 19:17 -------------------- Тот кто не знает и/или не понимает определений физических понятий - не знает физики.
То кто не знает физики - не знает и не понимает жизнь. Природу изучать не формулы тачать. |

|
|
 12.2.2018, 12:27 12.2.2018, 12:27
Сообщение
#12
|
|
|
Младший сержант    Группа: Старожилы Сообщений: 1837 Регистрация: 11.2.2018 Пользователь №: 200251 |
Я очень уважаю указанных вами авторов, "но истина дороже". И так из определения имеем: 1. Градиентом называется действие векторного оператора набла на скаляр. gradφ ≡ ∇φ. 2. Действие векторного оператора набла на вектор, согласно правилам векторного анализа возможен только в двух видах. А именно: а. Скалярное произведение векторного оператора на вектор есть дивергенция вектора divF ≡ (∇ ⋅ F); б. Векторное произведение векторного оператора набла на вектор есть ротор вектора. rotF ≡ [∇ Ч F]. А градиент вектора, это как? Здравствуйте уважаемый Зиновий. Зарегистрировался, когда у видел, что теперь вы тут модератор. Для меня основным является определение !. Для потенциального гравитационного поля функция поля U = GMm/R Размерность кг*метр2/сек2 - джоуль, скаляр. Градиент это производная (dGMm/R)/dr = -GMm/R2 = -ma вектор к центру сферы. Запись для потенциала U = GM/R не корректна. А что такое градиент вектора. Чтобы была производная, надо чтобы он был переменным. Например на плоскости модуль R = C*T угол Fi = w*T Угловая скорость на время. Производная по времени даст вектор С + вектор W Вектора взаимно перпендикулярны. Складывать такие вектора я не умею. Если конец вектора масса m, то могу сложить энергию E = mC2/2 + JW2/2 Энергия поступательно-вращательного движения. Перемножавшие даcт третий вектор. Перпендикулярный плоскости этих двух. А в объемных координатах, будет четвертое иизмерение? Энергии без массы не бывает. Так что там в электродинамике Максвелла вращается? Фиктивный вектор тока? |

|
|
 12.2.2018, 20:15 12.2.2018, 20:15
Сообщение
#13
|
|
 Прапорщик        Группа: Старожилы Сообщений: 7951 Регистрация: 14.8.2017 Пользователь №: 129274 |
Друзья, вы все здесь правы и не правы одновременно, а всё потому, что математика - это искусство называть одни и теже вещи разными именами (с) ...
По существу темы, нечто вразумительное можно почитать по ссылке: https://ru.m.wikipedia.org/wiki/Оператор_набла Посетить мою домашнюю страницу Хотя и там написана, в большей части, "абстрактная чепуха" (с) ... поразительно, но в теме о Числах мы всё это уже разбирали достаточно подробно ... Вот скажем это Действительно, в математике ОПРЕДЕЛЕНИЕ просто обязано быть предельно корректным и точным ... вот, например, по той же ссылке, которую я привёл выше, авторы рассуждают о каких-то операторах, забывая, что ОПЕРАТОР это синоним слова ОТОБРАЖЕНИЕ, и не более того, а что такое ОТОБРАЖЕНИЕ F в категории множеств это специального типа ОТНОШЕНИЕ, которое для наглядности принято записывать так: F: X --> Y И из этой записи нельзя ничего опустить ... нельзя сказать "просто оператор F", не указывая область определения оператора X и область его значений Y ... ибо, F: A --> B это будет ДРУГОЙ оператор, если только X или Y отличаются от A или В, соответственно, хотя бы даже одним элементом (точкой) ... тем более нелепо выглядит описание "оператора" "набла" без указания области определения и области его значений ... именно отсюда идут "оправдания" его использования как удобного символа некоторого "исчисления" ... такая метода восходит ещё к дифференциальному и интегральному ИСЧИСЛЕНИЮ Лейбница и Ньютона, когда выучив несколько табличных правил, можно "брать" производные и интегралы не зная что это такое, но так происходит до поры до времени, пока мы не сталкиваемся в тех же задачах естествознания с ситуацией что исчисление не работает для функций недифференцируемых (с "уголками") разрывных и т.п. всё это возникает уже в электротехнике (функция Хевисайда, дельта функция и т.п.), в том числе, и в так называемой теории поля, векторном анализе, а в новейшее время в Нелинейном Анализе и т.п. ... Как вы тут ссылки вставляете? ... :( Гиперссылки не работают ... чтобы посмотреть копируйте ссылку и вставляйте в строку браузера ... плохо ... Не понял юмора - почему в одних темах (например, о Числах) ссылки вставляются простым копированием, а здесь не вставляется ... Сообщение отредактировал Paraligon - 12.2.2018, 20:45 |

|
|
 13.2.2018, 5:24 13.2.2018, 5:24
Сообщение
#14
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7257 Регистрация: 12.8.2017 Пользователь №: 97485 |
Друзья, вы все здесь правы и не правы одновременно, а всё потому, что математика - это искусство называть одни и теже вещи разными именами (с) ... По существу темы, нечто вразумительное можно почитать по ссылке: Оператор_набла Посетить мою домашнюю страницу Хотя и там написана, в большей части, "абстрактная чепуха" (с) ... поразительно, но в теме о Числах мы всё это уже разбирали достаточно подробно ... Вот скажем это Действительно, в математике ОПРЕДЕЛЕНИЕ просто обязано быть предельно корректным и точным ... вот, например, по той же ссылке, которую я привёл выше, авторы рассуждают о каких-то операторах, забывая, что ОПЕРАТОР это синоним слова ОТОБРАЖЕНИЕ, и не более того, а что такое ОТОБРАЖЕНИЕ F в категории множеств это специального типа ОТНОШЕНИЕ, которое для наглядности принято записывать так: F: X --> Y И из этой записи нельзя ничего опустить ... нельзя сказать "просто оператор F", не указывая область определения оператора X и область его значений Y ... ибо, F: A --> B это будет ДРУГОЙ оператор, если только X или Y отличаются от A или В, соответственно, хотя бы даже одним элементом (точкой) ... тем более нелепо выглядит описание "оператора" "набла" без указания области определения и области его значений ... именно отсюда идут "оправдания" его использования как удобного символа некоторого "исчисления" ... такая метода восходит ещё к дифференциальному и интегральному ИСЧИСЛЕНИЮ Лейбница и Ньютона, когда выучив несколько табличных правил, можно "брать" производные и интегралы не зная что это такое, но так происходит до поры до времени, пока мы не сталкиваемся в тех же задачах естествознания с ситуацией что исчисление не работает для функций недифференцируемых (с "уголками") разрывных и т.п. всё это возникает уже в электротехнике (функция Хевисайда, дельта функция и т.п.), в том числе, и в так называемой теории поля, векторном анализе, а в новейшее время в Нелинейном Анализе и т.п. ... Как вы тут ссылки вставляете? ... :( Гиперссылки не работают ... чтобы посмотреть копируйте ссылку и вставляйте в строку браузера ... плохо ... Не понял юмора - почему в одних темах (например, о Числах) ссылки вставляются простым копированием, а здесь не вставляется ... Я здесь подправил. Вы наверное, поторопились со ссылками. -------------------- Felix qui potuit rerum cognoscere causas. /Вергилий/
Апейроника - наука будущего? |

|
|
 13.2.2018, 10:59 13.2.2018, 10:59
Сообщение
#15
|
|
 Прапорщик        Группа: Старожилы Сообщений: 7951 Регистрация: 14.8.2017 Пользователь №: 129274 |
vps137, спасибо, Друг! Я думаю, что большинство математиков ничего не понимают в связном наборе слов "векторный дифференциальный оператор" ... если кто и понимает, то требуется гораздо больше слов, чем написано в вики ...
Сообщение отредактировал Paraligon - 13.2.2018, 11:01 |

|
|
 13.2.2018, 12:22 13.2.2018, 12:22
Сообщение
#16
|
|
|
Рядовой  Группа: Пользователи Сообщений: 231 Регистрация: 21.1.2018 Пользователь №: 200238 |
Друзья, вы все здесь правы и не правы одновременно, а всё потому, что математика - это искусство называть одни и теже вещи разными именами (с) ... . Вот именно, создавать птичий язык, догматизируя то, что достигнуто моделированием в физике и устраивая из этого пляски абстракции ан костях познания. В динамике градиент/оператор набла имеет вид 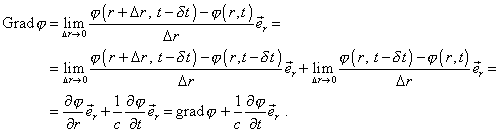 О градиенте потенциальной функции Это выражение получается физическим моделированием, но не может быть получено абстрактными математическими ухищрениями. При этом в динамике уже стандартное применение математических операторов rotgrad φ ≠ 0 И весь птичий язык переходит в пустое карканье. Развитие же математики возможно не придумыванием заумных слов, чем она, собственно, так увлеклась, а решением до сих пор не решённых задач в физике. Только тогда будет здоровое развитие, а не самолюбование. |

|
|
 13.2.2018, 13:19 13.2.2018, 13:19
Сообщение
#17
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7257 Регистрация: 12.8.2017 Пользователь №: 97485 |
Вот именно, создавать птичий язык, догматизируя то, что достигнуто моделированием в физике и устраивая из этого пляски абстракции ан костях познания. В динамике градиент/оператор набла имеет вид 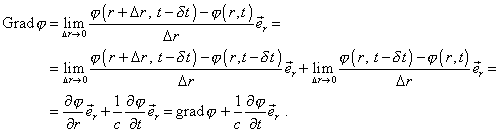 О градиенте потенциальной функции Это выражение получается физическим моделированием, но не может быть получено абстрактными математическими ухищрениями. При этом в динамике уже стандартное применение математических операторов rotgrad φ ≠ 0 И весь птичий язык переходит в пустое карканье. Развитие же математики возможно не придумыванием заумных слов, чем она, собственно, так увлеклась, а решением до сих пор не решённых задач в физике. Только тогда будет здоровое развитие, а не самолюбование. Здесь, Сергей, Вы, похоже, изобрели велосипед. Есть в математике понятие полной производной, которое близко к тому, что в Вас написано. [dmath] \frac {d \phi}{dt}=\dot \phi+(\vec u \cdot \nabla) \phi[/dmath] Если положить скорость u постоянной и равной c, то приходим к Вашему выражению. ([imath]\dot \phi=\frac{\partial \phi}{\partial t}[/imath]) Сообщение отредактировал vps137 - 13.2.2018, 13:26 -------------------- Felix qui potuit rerum cognoscere causas. /Вергилий/
Апейроника - наука будущего? |

|
|
 13.2.2018, 14:02 13.2.2018, 14:02
Сообщение
#18
|
|
|
Рядовой  Группа: Пользователи Сообщений: 231 Регистрация: 21.1.2018 Пользователь №: 200238 |
Здесь, Сергей, Вы, похоже, изобрели велосипед. Есть в математике понятие полной производной, которое близко к тому, что в Вас написано. [dmath] \frac {d \phi}{dt}=\dot \phi+(\vec u \cdot \nabla) \phi[/dmath] Если положить скорость u постоянной и равной c, то приходим к Вашему выражению. ([imath]\dot \phi=\frac{\partial \phi}{\partial t}[/imath]) Вот видите, как Вы переворачиваете, забыв, что в градиенте потенциала используются уже частные производные... ∇ = ex ∂ ∂x + ey ∂ ∂y + ez ∂ ∂z Что Вы можете после этого решить? Да, ничего. Только плескаться в догмате, играя словами. А между тем, если источник поля движется, будет уже другая формула... |

|
|
 13.2.2018, 14:05 13.2.2018, 14:05
Сообщение
#19
|
|
|
Прапорщик        Группа: Старожилы Сообщений: 7257 Регистрация: 12.8.2017 Пользователь №: 97485 |
А между тем, если источник поля движется, будет уже другая формула... Это тогда уж берите выше - ковариантная производная. Сообщение отредактировал vps137 - 13.2.2018, 14:06 -------------------- Felix qui potuit rerum cognoscere causas. /Вергилий/
Апейроника - наука будущего? |

|
|
 13.2.2018, 14:27 13.2.2018, 14:27
Сообщение
#20
|
|
|
Рядовой  Группа: Пользователи Сообщений: 231 Регистрация: 21.1.2018 Пользователь №: 200238 |
Это тогда уж берите выше - ковариантная производная. Опять игры в слова... Далее начнёте пространства изгибать, символы поднимать/опускать символом Кроннекера и проч. И здесь ковариантная? 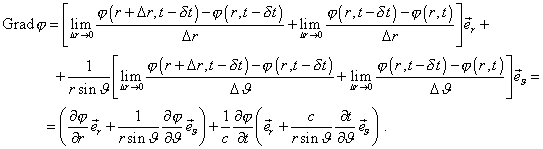 Это для движущегося источника (с. 7 статьи) А с учётом трансцендентного уравнения для самого запаздывания и этого не запишешь... А Вы говорите - велосипед... Ручка отмахнутая, а не велосипед.. |

|
|
  |
| Текстовая версия | Сейчас: 27.7.2024, 10:41 |